User Experience, Psychologie und Wahrnehmung II – Der Goldene Schnitt
Wenn es um User Experience geht, beschäftigt man sich häufig mit Fragen der Bedienung. Es geht darum, welche Buttons wann angeklickt werden, welche Textfelder zu befüllen sind, und wie sich Checkboxes am besten aktivieren lassen.
User Experience – die Nutzererfahrung – beginnt aber schon früher. Da es keine zweite Chance für den ersten Eindruck gibt, ist auch die Optik immer ein wesentlicher Aspekt. Wenn die Besucher einer Website sich schon beim ersten Anblick mit Grausen abwenden, kann die Benutzerführung noch so durchdacht und ausgeklügelt sein. Die Wenigsten werden sie jemals nutzen.
Das ist umso trauriger, als es in vielen Fällen nur eine simple Zahl und ein einfaches Konzept braucht, um etwas zu gestalten, das für das menschliche Auge schön und harmonisch anzusehen ist.
Der Goldene Schnitt, oder: Achtung, Mathematik!
Ein wichtiges Werkzeug für eine ansprechende Optik ist der Goldene Schnitt. Dieser Begriff klingt zwar sehr hochtrabend, tatsächlich handelt es sich aber lediglich um ein bestimmtes Teilungsverhältnis zweier Strecken:
Wenn zwei Strecken aneinandergefügt werden und das Verhältnis dieser neuen Strecke zur Längeren der beiden Ursprünglichen gleich dem Verhältnis dieser beiden Strecken zueinander ist, dann wird dieses Verhältnis als Goldener Schnitt bezeichnet.
Was nun etwas verschachtelt und in vielen Worten beschrieben wurde, lässt sich mathematisch folgendermaßen darstellen:
Die Strecken a und b (wobei a>b) bilden den Goldenen Schnitt, falls:
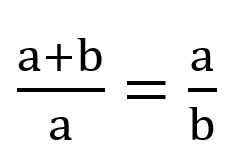
Dieses Teilungsverhältnis hat den Wert:
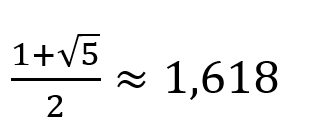
Anders gesagt: Wenn a ungefähr das 1,618-fache von b ist, so stehen die beiden Größen im Verhältnis des Goldenen Schnitts.
Fibonacci-Folge
Im Zusammenhang mit dem Goldenen Schnitt wird häufig die Fibonacci-Folge genannt. Dabei handelt es sich um eine Abfolge von Zahlen, bei denen jede die Summe ihrer beiden Vorgänger ist. In manchen Quellen wird dabei mit den beiden Zahlen 0 und 1 begonnen, in anderen mit 1 und 1.
Ausgehend von der Variante mit der Null am Anfang ergibt sich das nächste Element der Folge:
0+1=1
Damit hätten wir nun zwei Einsen und die Folge würde in beiden Varianten identisch fortgesetzt:
1+1=2
1+2=3
2+3=5
3+4=8 und so weiter.
Die so entstehende Abfolge an Zahlen wird als Fibonacci-Folge bezeichnet:
(0) – 1 – 1 – 2 – 3 – 5 – 8 – 13 – 21 – 34 – …
Fibonacci und der Goldene Schnitt
Bei Betrachtung der Zahlen in der Fibonacci-Folge ergibt sich rasch ein Zusammenhang mit dem Goldenen Schnitt:
Nehmen wir a=13 und b=8. Das nächste Element der Fibonacci-Folge wäre damit a+b=21
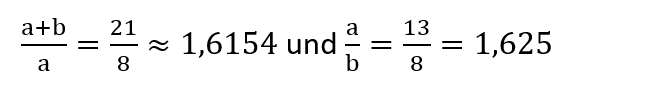
Die beiden Divisionen liefern schon fast das gleiche Ergebnis, aber noch nicht ganz. Den Goldenen Schnitt haben wir also (noch) knapp verfehlt.
Führen wir aber die gleiche Rechnung mit den Fibonacci-Zahlen 610 und 987 durch, sind die Verhältnisse schon recht ähnlich. Mit ca. 1,6180344 und 1,6180328 stimmen immerhin schon die ersten fünf Nachkommastellen überein. Diese Tendenz setzt sich weiter fort. Je größer die Fibonacci Zahlen werden, umso mehr nähert sich ihr Verhältnis zueinander dem Goldenen Schnitt an.
Design, Harmonie und da Vinci
Was ist aber nun das Besondere an dieser merkwürdigen Zahl, die einen Wert von ungefähr 1,618 hat?
Sie stellt ein Verhältnis dar, das für das menschliche Auge als besonders schön und harmonisch gilt. Es ist kein Zufall, dass viele Kunstwerke auf dieses Teilungsverhältnis zurückgreifen.
Ein bekanntes Beispiel ist die Skizze des »Vitruvianischen Menschen« von Leonardo da Vinci. Sie zeigt einen Mann, dessen ausgestreckte Arme und Beine in jeweils zwei Positionen dargestellt werden und dabei sowohl ein umgebendes Quadrat als auch einen Kreis berühren. Dabei stehen sowohl die Maße des Bildes insgesamt wie auch jene des Kreises und des Quadrats annähernd im Verhältnis des Goldenen Schnitts. Gleiches gilt für die Proportionen der verschiedenen Körperteile des Mannes zueinander.

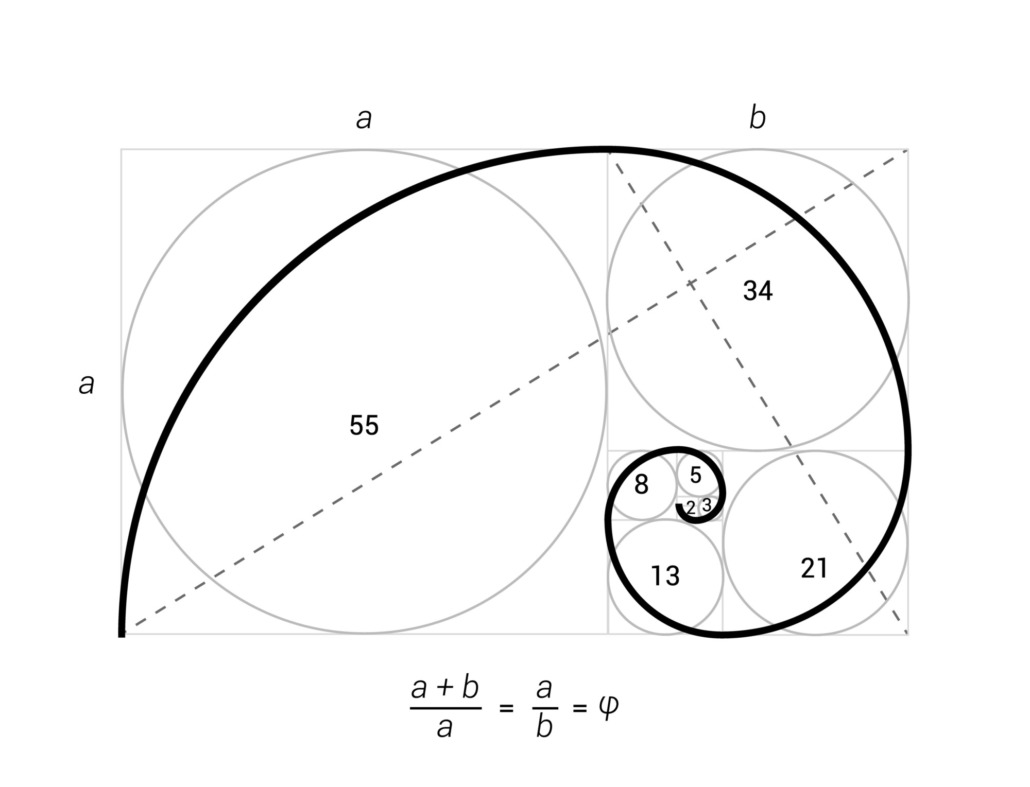
Ein anderes Beispiel, bei dem wieder der gute Fibonacci herhalten muss, ist die Fibonacci-Spirale. Dabei wird eine Anordnung von Quadraten und Rechtecken gebildet, in der sich eine Spiralform erkennen lässt. Da die Seitenlängen dieser Vierecke jeweils den Fibonacci-Zahlen entsprechen, nähern sich deren Verhältnisse zueinander wieder dem Goldenen Schnitt an. Diese Vierecke lassen sich so anordnen, dass sich eine Spirale darüberlegen lässt
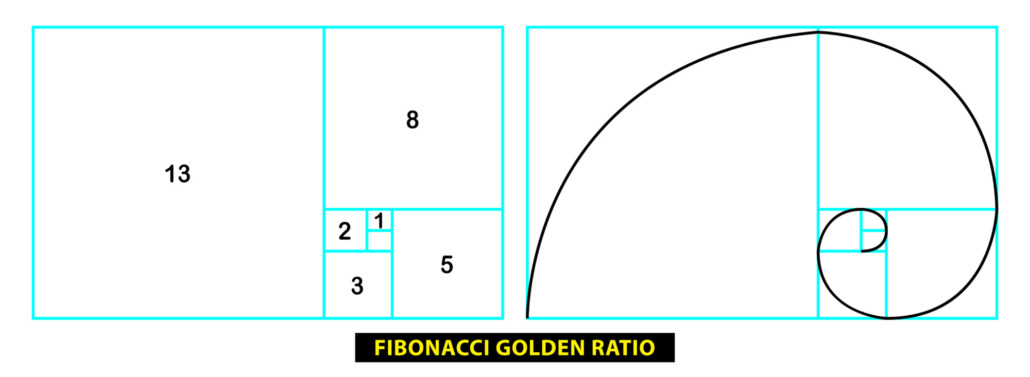
Diese Form findet sie häufig in der Natur wieder, etwa beim Aufbau von Schneckenhäusern. Auch in der Anordnung der Samen in der Blüte einer Sonnenblume lassen sich mehrere ineinander verschachtelte Fibonacci-Spiralen erkennen.

Und wie nutze ich den Goldenen Schnitt?
Wenn mehrere Elemente gemeinsam dargestellt werden sollen, wie etwa Textblöcke und Bilder auf einer Website, mag manch einer im ersten Impuls dazu neigen, sie symmetrisch anzuordnen. Das mag zwar auch eine gewisse Harmonie entwickeln, wirkt aber bald statisch und langweilig. Gerade die Vermeidung von Symmetrien bietet im Gegensatz dazu eine gewisse Lebendigkeit. Dabei hat sich der Goldene Schnitt als ideales Teilungsverhältnis entpuppt.
Du willst also Text und Bild gemeinsam anzeigen? Warum nicht den Textblock ca. 1,618-mal so breit wie das Bild darstellen. Oder vielleicht liegen dir auch zwei Bilder vor, die du so skalieren kannst, dass ihre Breiten im Verhältnis des Goldenen Schnitts zueinanderstehen.
Erinnern wir uns an die Gestaltgesetze im vorhergehenden Beitrag, insbesondere an das Gesetz der Nähe: Wenn wir aus den darzustellenden Elementen Gruppen bilden, die thematisch zusammengehören, können wir auch dabei den Goldenen Schnitt anwenden, beispielsweise durch Bildung von Spalten. Das nachfolgende Bild skizziert einen dreigeteilten Aufbau, bei dem die Höhen der einzelnen »Spalten« jeweils ein Verhältnis von ca. 1:1,618 zueinander haben.

Was für eine vertikale Aufteilung gilt, lässt sich natürlich auch in der Horizontalen anwenden. Je nachdem, ob beispielsweise ein stationärer Monitor im „Querformat“ zum Einsatz kommt, oder ein mobiles Gerät, das in „aufrechter“ Position gehalten wird, kannst du dir entweder im Zusammenhang mit den Höhen oder den Breiten Gedanken über den Goldenen Schnitt machen.
Häufig sind aber Elemente nicht nur nebeneinander oder nur übereinander angeordnet. In solchen Fällen lässt sich der Goldene Schnitt in Gestalt der Fibonacci-Spirale anwenden. Dabei orientieren sich die einzelnen Teile an ihrem Verlauf. Auf vielen Seiten findet sich (teilweise auch sowohl horizontal als auch vertikal gespiegelt) eine Anordnung, die an folgende Illustration erinnert.
Abschließend sollte auch erwähnt werden, dass sich die Anwendung des Goldenen Schnitts und der Fibonacci-Spirale nicht nur auf Websites beschränkt. Auch bei der Gestaltung von Zeitschriften oder Flyern oder in der Fotografie kommen diese Konzepte zum Einsatz bzw. werden berücksichtigt.
Das könnte dich auch interessieren

Günter Gerstbrein
Günter Gerstbrein, Jahrgang 1977, studierte technische Mathematik an der TU Wien und war etwa 13 Jahre in der Software-Entwicklung tätig. Als „Texter, der aus der Technik kam“ ist es sein Ziel, komplizierte Sachverhalte leicht verständlich und ohne viel Techno-Babble zu vermitteln.







